Логика и отрезки. Решения.
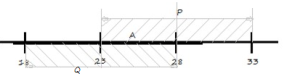
№1 На числовой прямой даны два отрезка: P = [23, 33] и Q = [18,28]. Определите возможную максимальную длину отрезка А, что обе формулы
(x ∉ P) ∧ (x ∈ A)
(x ∉ Q) ∧ (x ∈ A)
тождественно ложны, то есть принимают значение 0 при любом значении переменной х.
Решение
Утверждение тождественно ложно тогда и только тогда, когда его отрицание тождественно истинно. Запишем отрицания заданных утверждений. Рассмотрим сначала выражение (x ∉ P) ∧ (x ∈ A). Оно ложно, когда (x ∈ P) или (x ∉ A), т.е., когда истинно (x ∈ P) ∨(x ∉ A), что эквивалентно (x ∈ A) →(x ∈ P) . Последнее выражение истинно для всех x тогда и только тогда, когда
A ⊆P (1.1)
Аналогично, из того, что тождественно ложно выражение (x ∉ Q) ∧ (x ∈ A), получаем
A ⊆Q (1.2)
Конъюнкция (1.1) и (1.2) эквивалентна
A ⊆P ⋂ Q (1.3)
Из (1.3) следует, что максимальная длина отрезка A равна длине отрезка P ⋂Q = [23, 28], т.е. 28-23 = 5.
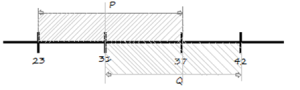
№2 На числовой прямой даны два отрезка: P = [23, 37] и Q = [31 , 42]. Определите возможную максимальную длину отрезка А, что обе формулы
(x ∈ P) ∨ (x ∉ A)
(x ∈ Q) ∨ (x ∉ A)
тождественно истинны, то есть принимают значение 1 при любом значении переменной х.
Решение
По условию требуется, чтобы оба выражения были тождественно истинны. Рассмотрим сначала выражение (x ∈ P) ∨(x ∉ A), что эквивалентно (x ∈ A) →(x ∈ P). Последнее выражение истинно для всех x тогда и только тогда, когда
A ⊆P (2.1)
Аналогично, для выражения (x ∈ Q) ∨ (x ∉ A), получаем
A ⊆Q (2.2)
Конъюнкция (2.1) и (2.2) эквивалентна
A ⊆P ⋂Q (2.3)
Из (2.3) следует, что максимальная длина отрезка A равна длине отрезка P ⋂Q = [31, 37], т.е. 37-31 = 6.
№3 На числовой прямой даны два отрезка: Р = [25, 45] и Q = [15, 55]. Отрезок А таков, что логические выражения
(х ∈ P) → (х ∈ А)
(х ∈ А) → (х ∈ Q)
тождественно истинны, то есть принимают значение 1 при любом значении переменной х.
Какова максимальная возможная длина отрезка А?
Решение
По условию требуется, чтобы оба выражения были тождественно истинны. Рассмотрим сначала выражение (х ∈ P) → (х ∈ А), которое истинно для всех x тогда и только тогда, когда
P ⊆A (3.1)
Аналогично, выражение (х ∈ А) → (х ∈ Q) истинно, когда
A ⊆Q (3.2)
Конъюнкция (3.1) и (3.2) эквивалентна
P ⊆ A ⊆ Q (3.3)
Т.к. P ⊆ Q, то из (3.3) следует, что максимальная длина отрезка A равна длине отрезка A=Q = [15, 55], т.е. 55-15 = 40.
Отметим, что, если не выполнено условие P ⊆ Q, то задача не имеет решения.
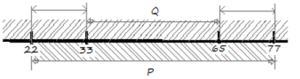
№4 На числовой прямой даны два отрезка: Р = [22, 77] и Q = [33, 65]. Отрезок А таков, что логические выражения
(х ∈ А) → (х ∈ P)
(х ∈ Q) → (х ∈ А)
тождественно истинны, то есть принимают значение 1 при любом значении переменной х.
Какова минимальная возможная длина отрезка А?
Решение
См. решение задания №3.
№5 На числовой прямой даны два отрезка: Р = [22, 77] и интервал Q = (33, 65). Отрезок А таков, что логические выражения
(х ∈ А) → (х ∈ P)
(x ∉ Q) ∨ (x ∉ A)
тождественно истинны, то есть принимают значение 1 при любом значении переменной х.
Какова максимальная возможная длина отрезка А?
Решение
По условию нам надо, чтобы оба выражения были тождественно ложны. Рассмотрим сначала выражение (х ∈ А) → (х ∈ P). Оно истинно для всех x тогда и только тогда, когда
A ⊆P (5.1)
Второе выражение (x ∉ Q) ∨ (x ∉ A) эквивалентно (х ∈ А) → (x ∉ Q). Последнее истинно, когда
A ⊆¬Q, (5.2)
Здесь ¬Q обозначает дополнение интервала Q, т.е. (5.2.) эквивалентно
A ⊆ (-∞,33] ∨A ⊆ [65, +∞) (5.3)
Конъюнкция (5.1) и (5.3) эквивалентна
A ⊆(-∞,33] ⋂ P ∨ A ⊆[65, +∞) ⋂ P
A ⊆ [22,33] ∨ A ⊆ [65,77] (5.4)
Т. к. надо выбрать отрезок A так, чтобы его длина была максимальна, то нам подходит отрезок [65,77]. Получаем, что максимальная длина отрезка A равна длине отрезка [65, +∞) ⋂ P=[65,77], т. е. 77-65=12.
Ответ: 12.


0 Comments
Оставьте коммент первым.