Задание 9
4. Задачи для самостоятельного решения
5. Дополнение. Некоторые сведения о цифровой звукозаписи.
6. Решения задач с сайта ege.yandex.ru
1. Общие сведения
Сложность: базовая.
Примерное время решения (для тех, кто будет выполнять часть 2): 2 минуты
Тема: Создание и обработка графической и мультимедийной информации
Подтема: Цифровая звукозапись
Что проверяется: Умение оценивать количественные характеристики процесса записи звука.
Краткие теоретические сведения: Поскольку данный тип задания является новым в КИМ ЕГЭ, приведем (пока без обоснования, обоснование ниже) математическую модель процесса звукозаписи:
N = k * F * L *T (1)
где
- • N – размер файла (в битах) , содержащего запись звука;
- • k - количество каналов записи (например, 1 – моно, 2 – стерео, 4 – квадро и т.д.);
- • F – частота дискретизации (в герцах), т.е. количество значений амплитуды звука фиксируемых за одну секунду;
- • L – разрешение, т.е. число бит, используемых для хранения каждого измеренного значения;
- • T – продолжительность звукового фрагмента (в секундах).
Как может выглядеть задание? Например, так: Заданы значения всех требуемых параметров процесса звукозаписи, кроме одного. Требуется оценить значение оставшегося параметра, например, размер файла или продолжительность звукового фрагмента.
Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
Варианты ответов:
1) 0,2 Мбайт
2) 2 Мбайт
3) 3 Мбайт
4) 4 Мбайт
2. Пример задания
2.1. Условие задачи.
Задача 2012-А8-1.
Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 0,2 Мбайт 2) 2 Мбайт 3) 3 Мбайт 4) 4 Мбайт
2.2. Решение.
Приводим исходные данные к размерности биты-секунды-герцы и проводим расчеты по формуле (1):
Дано:
k = 1, т.к. одноканальная (моно) звукозапись;
F = 16 кГц = 16 000 Гц;
L = 24;
T = 1 мин = 60 с.
Найти N
Подставляем значение известных параметров в формулу (1)
N = 1*16000*24*60 =(16*1000)* (8*3) * (4*15)=
= 24*(23*125)*(23*3)* )*(22* 15) = 212*5625 (бит)=
= 212*5625 бит = (212*5625)/23 байт = 29*5625 байт =
= (29*5625)/ 220 Мбайт = 5625/211 Мбайт = 5625/2048 Мбайт.
Число 5625/2048 находится между числами 2 и 3. При этом оно ближе к 3, чем к 2, т.к. 3 * 2048 – 5625 < 1000; 5625 - 2 * 2048 > 1000.
Правильный вариант ответа: №3 (3 Мбайт)
Замечание. Другая идея решения приведена в п.3.3
3. Советы учителям и ученикам
3.1 Какие знания/умения/навыки нужны ученику, чтобы решить эту задачу
1) Не следует «зазубривать» формулу (1). Ученик, представляющий суть процесса цифровой звукозаписи, должен быть способен самостоятельно её сформулировать.
2) Необходимо умение записывать значения параметров в требуемой размерности, а также элементарные арифметические навыки, в т.ч. оперирование со степенями двойки.
3.2. Рекомендации для учителей: как разбирать задачу с учениками
Эти рекомендации – не догма, а попытка сделать выводы из собственного опыта. Ждем комментариев и Ваших рекомендаций.
А. Сильные ученики.
1. Скорее всего, они и так решат эту задачу.
2. Можно дать задание ученикам проверить формулу (1) на практике, записывая в файл звук с микрофона. При этом следует учесть, что она справедлива только в том случае, если записываемая информация не подвергается сжатию (формат WAV (PCM) без сжатия). Если используются аудиоформаты со сжатием (WMA, MP3), то объем получившегося файла будет по понятным причинам существенно меньше расчетного. Для экспериментов с цифровой звукозаписью можно использовать свободно распространяемый аудиоредактор Audacity (http://audacity.sourceforge.net/).
3. Целесообразно подчеркнуть концептуальную общность растрового представления звука и изображения, являющихся разновидностями одного и того же процесса приближенного представления непрерывного сигнала последовательность коротких дискретных сигналов, т.е. оцифровывания на основе дискретизации. В случае растрового изображения производится двумерная дискретизизация яркости в пространстве, в случае звука – одномерная дискретизация по времени. И в том, и в другом случае повышение частоты дискретизации (количества пикселей или звуковых отсчетов) и/или увеличение количества битов для представления одного отсчета (разрядность цвета или звука) ведет к повышению качества оцифровки, при одновременном росте размера файла с цифровым представлением. Отсюда – необходимость сжатия данных.
4. Желательно упомянуть об альтернативных способах оцифровки звука – запись «партий» инструментов в MIDI-формате. Здесь уместно провести аналогию с растровым и векторным представлением изображений.
Б. Не столь сильные ученики.
1. Необходимо обеспечить усвоение соотношения (1). Рекомендуется дать задания типа «Как изменится объем файла, если время записи звучания увеличить/уменьшить в p раз? »,
«Во сколько раз можно увеличить/уменьшить продолжительность записи, если максимальный размер файла увеличить/уменьшить в p раз? », «Как изменится объем файла, если количество бит для записи одного значения увеличить/уменьшить в p раз?» и т.д.
2. Необходимо убедиться, что учащиеся свободно оперируют размерностями, знают, что в Мбайте 223 бит и т.д.
3. Необходимо убедиться, что учащиеся достаточно арифметически грамотны, свободно владеют устным счетом со степенями двойки (умножение, деление, выделение сомножителей, представляющих собой 2n).
4. Придумывайте свои подходы и пробуйте их.
3.3. Полезный прием.
В подобных задачах часто возникают степени двойки. Перемножать и делить степени проще, чем произвольные числа: умножение и деление степеней сводится к сложению и вычитанию показателей.
Заметим, что числа 1000 и 1024 отличаются менее, чем на 3%, числа 60 и 64 отличаются менее, чем на 7%. Поэтому можно поступить так. Провести вычисления, заменив 1000 на 1024 = 210 и 60 на 64 = 26, используя преимущества операций со степенями. Ближайший к полученному числу ответ и будет искомым. Можно после этого перепроверить себя, проведя точные вычисления. Но можно учесть, что общая погрешность вычислений при нашем приближении не превышает 10%. Действительно, 60*1000 = 60000; 64*1024=65536;
60000 > 0.9 * 65536 = 58982.4
Таким образом, правильный результат умножений по формуле (1) немного больше, чем 90% от полученного приближенного результата. Если учет погрешности не меняет результата – можно не сомневаться в ответе.
Пример. (ege.yandex.ru, вариант 1).
Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 30 Мбайт 2) 60 Мбайт 3) 75 Мбайт 4) 90 Мбайт
Решение. Размер записи в битах равен
2*16*1000*32*12*60
С учетом замены 1000 на 1024=210 и 60 на 64=26 получим:
21*24*210*25*3*22*26=3*228
Как известно, 1 Мбайт = 220 байт = 223 бит. Поэтому 3*228 бит = 3*32 = 96 Мбайт. Уменьшив это число на 10%, получим 86.4 Мбайт. В обоих случаях ближайшей величиной является 90 Мбайт.
Правильный ответ: 4
3.4. Рекомендации для учеников: как решать подобные задачи
1. Прочитайте условие задачи. Выразите неизвестный параметр через известные. Особое внимание обратите, на размерность известных параметров. Она должна быть – биты-секунды-герцы (напомним, что 1 Гц = с-1). При необходимости, приведите значения параметров к нужной размерности, так же как это делается в задачах по физике.
2. Проводите вычисления, стараясь выделять степени двойки.
3. Обратите внимание, что в условии требуется выбрать наиболее подходящий ответ, поэтому высокая точность вычислений до знаков после запятой не требуется. Как только стало ясно, какой из вариантов ответов наиболее близок к вычисляемому значению, вычисления следует прекратить. Если расхождение со всеми вариантами ответов очень велико (в разы или на порядок), то вычисления надо перепроверить.
Удачи!
4. Задачи для самостоятельного решения
4.1. Клоны задачи 2012-А8-1.
Ниже приведены еще четыре варианта задачи 2012-А8-1.
А) Производится одноканальная (моно) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 15 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт
Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 30 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт
В) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт
Г) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 4 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт
Правильные ответы:
А:1; Б:3; В:3; Г:4.
4.2. Задача 2012-А8-2(обратная к предыдущей).
A) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?
1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд
Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?
1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд
В) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 8-битным разрешением. Результаты записываются в файл, размер которого не может превышать 2,5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?
1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд
Г) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 16-битным разрешением. Результаты записываются в файл, размер которого не может превышать 5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?
1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд
Правильные ответы:
А:3; Б: 4 ; В: 1; Г:1 .
5.Дополнение. Некоторые сведения о цифровой звукозаписи.
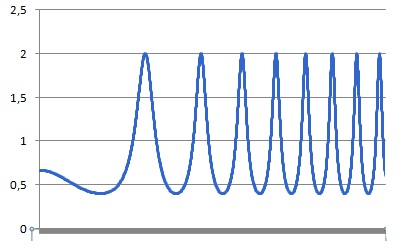
Распространение звука в воздухе можно рассматривать как распространение колебаний давления. Микрофон преобразует колебания давления в колебания электрического тока. Это аналоговый непрерывный сигнал. Звуковая плата обеспечивает дискретизацию входного сигнала от микрофона. Это делается следующим образом – непрерывный сигнал заменяется последовательностью измеренных с определенной точностью значений.
Пример:
График аналогового сигнала:
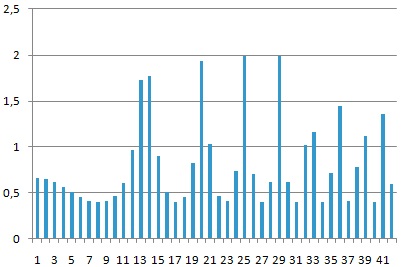
Дискретное представление этого же сигнала (41 измеренное значение):
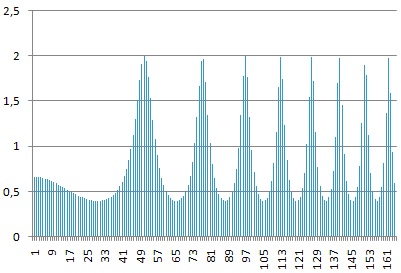
Дискретное представление этого же сигнала (161 измеренное значение, более высокая частота дискретизации):
Видно, что чем выше частота дискретизации, тем выше качество приближенного (дискретного) сигнала. Кроме частоты дискретизации, на качество оцифрованного сигнала влияет количество двоичных разрядов, отводимых для записи каждого значения сигнала. Чем больше бит отводится под каждое значение, тем более точно можно оцифровать сигнал.
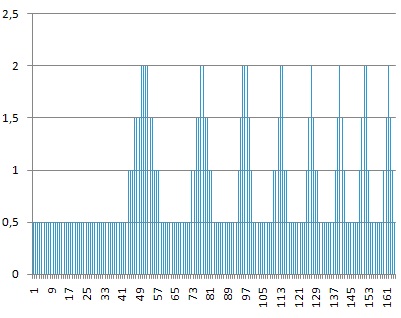
Пример 2-х битного представления этого же сигнала (двумя разрядами можно пронумеровать только 4 возможных уровня величины сигнала):
Теперь можно выписать зависимость для размера файла с оцифрованным звуком
размер_файла = (количество_значений,_фиксируемых_за_1_секунду)*
*( количество_двоичных_разрядов_для_записи_одного_значения )*
*(число_секунд_записи).
Учитывая возможность одновременной записи звука с нескольких микрофонов (стерео-, квадро- запись и т.д.), что делается для усиления реалистичности при воспроизведении, получаем формулу (1).
При воспроизведении звука цифровые значения преобразуются в аналоговые. Электрические колебания, передаваемые на динамики, преобразуются ими снова в колебания давления воздуха.


0 Comments
Оставьте коммент первым.