Задание 15. Ответы и решения
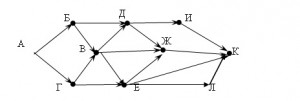
15.1 ( ege.yandex.ru – 1) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение 1. Это решение основывается на следующем правиле.
Правило сложения. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину К, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от К к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей |
Обратите внимание: вершину В нужно просмотреть раньше, чем вершины Б и Г, поскольку в графе есть ребра БВ и ГВ. А в каком порядке рассматривать вершины в тройке И, Л, Ж или паре Е и Д – не важно.
Из вершины К есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Для каждой из вершин И, Ж, Л есть ровно 1 путь в К.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 1 |
Для вершина Д – два пути, а для вершины Е – три пути.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 |
А дальше, чтобы не запутаться, будем использовать правило явно. Получим:
NВ = NД + NЖ + NЕ = 2+1+3 = 6
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 |
NБ = NВ + NД = 6+2 = 8
NГ = NВ + NЕ = 6+3 = 9
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 8 | 9 |
NА = NБ + NВ = 8+9 = 17
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | Л | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 8 | 9 |
Ответ: 17
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | И | Ж | Л | Е | Д | В | Г | Б | А |
| Куда идем | - | К | К | К | Ж,Л, К | И,Ж | Д,Е,Ж | В,Е | В,Д | Б,В,Г |
| К-во путей | 1 |
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вершина | К | И | Ж | Л | Е | Д | В | Г | Б | А |
| Куда идем | - | К | К | К | Ж,Л, К | И,Ж | Д,Е,Ж | В,Е | В,Д | Б,В,Г |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 9 | 8 | 17 |
Например, 7-й столбец (вершина В) заполняем так. В строке «Куда идем» - 3 вершины Д, Е, Ж. Значит, по правилу сложения,
NВ = NД + NЕ + NЖ = 2+3+1=6
Количества путей NД, NЕ, NЖ для вершин Д, Е, Ж были записаны в строку «К-во путей» раньше.
Ответ: 17
Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные.
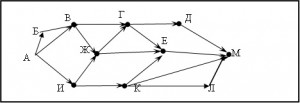
15.2 ( ege.yandex.ru – 2) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение 1. Это решение основывается на следующем правиле. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину М, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от М к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей |
Обратите внимание: вершину Е нужно просмотреть раньше, чем вершину К, поскольку в графе есть ребро КЕ. А в каком порядке рассматривать вершины в тройке Д, Е, Л – не важно.
Из вершины М есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Для каждой из вершин Д, Е, Л есть ровно 1 путь в М
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 |
Для вершины Г – два пути, а для вершины К – три пути.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 |
А дальше, чтобы не запутаться, будем использовать правило явно. Получим:
NЖ = NГ + NЕ = 2+1 = 3
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 3 |
NВ = NГ + NЖ = 2+3 = 5
NБ = NВ = 5
NИ = NЖ + NК = 3+3 = 6
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 5 | 6 | 5 |
NА = NБ + NВ + NК = 5+5+6 = 16
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 5 | 6 | 5 | 16 |
Ответ: 16
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К | Г | Ж | В | И | Б | А |
| Куда идем | - | М | М | М | Е,Л,М | Д,Е | Г,Е | Г,Ж | Ж,К | В | Б,В,И |
| К-во путей | 1 |
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К | Г | Ж | В | И | Б | А |
| Куда идем | - | М | М | М | Е,Л,М | Д,Е | Г,Е | Г,Ж | Ж,К | В | Б,В,И |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 5 | 6 | 5 | 16 |
Например, 8-й столбец (вершина В) заполняем так. В строке «Куда идем» - 2 вершины Г, Ж. Значит, по правилу сложения,
NВ = NГ + NЖ = 2 +3=5
Количества путей NГ, NЖ для вершин Г, Ж были записаны в строку «К-во путей» раньше.
Ответ: 16
Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные.
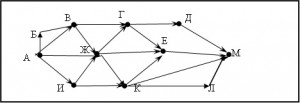
15.3 ( ege.yandex.ru – 3) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение 1. Это решение основывается на следующем правиле. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину М, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от М к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
|
|
|
|
|
|
|
|
|
|
|
Обратите внимание: вершину Е нужно просмотреть раньше, чем вершину К, поскольку в графе есть ребро КЕ. А в каком порядке рассматривать вершины в тройке Д, Е, Л – не важно.
Из вершины М есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Для каждой из вершин Д, Е, Л есть ровно 1 путь в М
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
Для вершины Г – два пути, а для вершины К – три пути.
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
1 |
1 |
1 |
1 |
3 |
2 |
|
|
|
|
|
А дальше, чтобы не запутаться, будем использовать правило явно. Получим:
NЖ = NГ + NЕ = 2+1 = 3
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
1 |
1 |
1 |
1 |
3 |
2 |
3 |
|
|
|
|
NВ = NГ + NЖ = 2+3 = 5
NБ = NВ = 5
NИ = NЖ + NК = 3+3 = 6
|
№ просмотра |
1 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
1 |
1 |
1 |
1 |
3 |
2 |
3 |
5 |
6 |
5 |
|
NА = NБ + NВ + NИ = 5+5+6+3 = 19
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Л |
Е |
Д |
К |
Г |
Ж |
В |
И |
Б |
А |
|
К-во путей |
1 |
1 |
1 |
1 |
3 |
2 |
3 |
5 |
6 |
5 |
19 |
Ответ: 19
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Д |
Л |
Е |
К |
Г |
Ж |
В |
И |
Б |
А |
|
Куда идем |
- |
М |
М |
М |
Е,Л,М |
Д,Е |
Г,Е |
Г,Ж |
Ж,К |
В |
Б,В,:Ж, И |
|
К-во путей |
1 |
|
|
|
|
|
|
|
|
|
|
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
|
№ просмотра |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершина |
М |
Д |
Л |
Е |
К |
Г |
Ж |
В |
И |
Б |
А |
|
Куда идем |
- |
М |
М |
М |
Е,Л,М |
Д,Е |
Г,Е |
Г,Ж |
Ж,К |
В |
Б,В,:Ж, И |
|
К-во путей |
1 |
1 |
1 |
1 |
3 |
2 |
3 |
5 |
6 |
5 |
19 |
Например, 8-й столбец (вершина В) заполняем так. В строке «Куда идем» - 2 вершины Г, Ж. Значит, по правилу сложения,
NВ = NГ + NЖ = 2 +3=5
Количества путей NГ, NЖ для вершин Г, Ж были записаны в строку «К-во путей» раньше.
Ответ: 19
Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные.
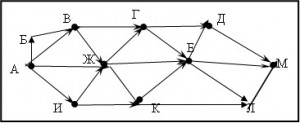
15.4 ( ege.yandex.ru – 4) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение 1. Это решение основывается на следующем правиле. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину М, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от М к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей |
Обратите внимание: вершину Е нужно просмотреть раньше, чем вершину К, поскольку в графе есть ребро КЕ. А в каком порядке рассматривать вершины в тройке Д, Е, Л – не важно.
Из вершины М есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Для каждой из вершин Д, Е, Л есть ровно 1 путь в М
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 |
Для вершины Г – два пути, а для вершины К – три пути.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 |
А дальше, чтобы не запутаться, будем использовать правило явно. Получим:
NЖ = NГ + NЕ + NК = 2+1+3 = 6
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 |
NВ = NГ + NЖ = 2+6 = 8
NБ = NВ = 8
NИ = NЖ + NК = 6+3 = 9
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 8 | 9 | 8 |
NА = NБ + NВ + NЖ + NИ = 8+8+6+9 = 31
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Е | Д | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 8 | 9 | 8 | 31 |
Ответ: 31
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
/p
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К |
Г |
Ж | В | И | Б | А |
| Куда идем | - | М | М | М | Е,Л,М | Д,Е | Г,Е,К | Г,Ж | Ж,К | В |
Б,В,:Ж, И |
| К-во путей | 1 |
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К | Г | Ж | В | И | Б | А |
| Куда идем | - | М | М | М | Е,Л,М | Д,Е | Г,Е,К | Г,Ж | Ж,К | В | Б,В,:Ж, И |
| К-во путей | 1 | 1 | 1 | 1 | 3 | 2 | 6 | 8 | 9 | 8 | 31 |
Например, 8-й столбец (вершина В) заполняем так. В строке «Куда идем» - 2 вершины Г, Ж. Значит, по правилу сложения,
NВ = NГ + NЖ = 2 +6=8
Количества путей NГ, NЖ для вершин Г, Ж были записаны в строку «К-во путей» раньше.
Ответ: 31
Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные
15.5 ( ege.yandex.ru – 5) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении/td, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение 1. Это решение основывается на следующем правиле. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину М, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от М к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей |
Обратите внимание: вершину Д нужно просмотреть раньше, чем вершину Е, поскольку в графе есть ребро ЕД. А в каком порядке рассматривать вершины в паре Д, Л – не важно.
Из вершины М есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Для каждой из вершин Д, Л есть ровно 1 путь в М; из вершины Е – 3 пути
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 3 |
Дальше, чтобы не запутаться, будем использовать правило сложения явно
NГ = NД + NЕ = 1+3 = 4
NК = NЛ + NЕ = 1+3 = 4
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 3 | 4 | 4 |
NЖ = NГ + NЕ + NК = 4+3+4 = 11
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 3 | 4 | 4 | 10 |
NВ = NГ + NЖ = 4+11 = 15
NБ = NВ = 15
NИ = NЖ + NК = 11+4 = 15
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 3 | 4 | 4 | 11 | 15 | 15 | 15 |
NА = NБ + NВ + NЖ + NИ = 15+15+11+15 = 56
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Л | Д | Е | К | Г | Ж | В | И | Б | А |
| К-во путей | 1 | 1 | 1 | 3 | 4 | 4 | 11 | 15 | 15 | 15 | 56 |
Ответ: 56
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К | Г | Ж | В | И | Б | А |
| Куда идем | - | М | М | Д,Л,М | Е,Л | Д,Е | Г,Е,К | Г,Ж | Ж,К | В | Б,В,Ж,И |
| К-во путей | 1 |
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Вершина | М | Д | Л | Е | К | Г | Ж | В | И | Б | А |
| Куда идем | - | М | М | Д,Л,М | Е,Л | Д,Е | Г,Е,К | Г,Ж | Ж,К | В | Б,В,Ж,И |
| К-во путей | 1 | 1 | 1 | 3 | 4 | 4 | 11 | 15 | 15 | 15 | 56 |
Например, 7-й столбец (вершина Г) заполняем так. В строке «Куда идем» - 2 вершины Д, Е. Значит, по правилу сложения,
NГ = NД + NЕ = 1 + 3=4
Количества путей NД, NЕ для вершин Д, Е были записаны в строку «К-во путей» раньше.
Ответ: 56
Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные.
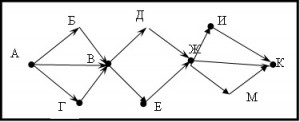
15.6 На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение Любой путь из А в М проходит сначала через В, а потом через Ж. Из А в В есть 3 пути, из В в Ж есть 2 пути, из Ж в М есть 3 пути. Значит, из А в М есть 3*2*3 = 18 путей.
Ответ: 18



14 комментариев
И почему умножаем а не прибавляем в последнем задании?
Че то нифига не поняла в последнем задании! По решению дорога должна быть из К в М, а в задании и М в К ! Че к чему?!
Офигенный сайт, я ни разу таких сайтов не встречала! РЕСПЕКТ вам от чистого сердца! 🙂
Я схожу с ума....
Держись! Ты нам нужен!
Задавай конкретные вопросы. Или иди отдыхать - на экзамене лучше быть свежим 🙂
http://ege-go.ru/zadania/grb/b9/b9-answ/#B9.2
31 просто быть не может! верный ответ 17!
Ты зачем постишь коммент 3 раза?! 🙂
Кроме того: ты даешь ссылку на B9.2, а ответ 31 - в B9.4
Кроме того: почитай решение (там из по 2 на каждую задачу) и напиши кокретно, что тебе непонятно 🙂
Удачи!
Здравствуйте. вы извините меня, пожалуйста, но у меня возник вопрос один. Вы можете написать решение А1, вот как оно выглядит:
Сколько единиц в шестнадцатеричной записи десятичного числа 497,5?
Вдруг на ЕГЭ попадется, а я не знаю как решать?
ошибочка вышла, всё таки там 16 а не 17)
А ты говоришь...:)
Удачи!
http://ege-go.ru/zadania/grb/b9/b9-answ/#B9.2
у меня вообще 17 вариантов от А до М получилось, кто больше? =)
Не кто больше, а кто меньше? 🙂
Посмотри решение на сайте - вроде, там ошибки нет.
Ты заполнял таблицу или выписывал пути? Пришли свое решение - разберемся
Вы извините, но у вас еще одна опечатка B9.2
NА = NБ + NВ + NК = 5+5+6 = 16. Там надо написать NA = NБ + NB + NИ = 16. Потому что, пункт К в самом конце и до него одним ходом не добраться, и к тому же в таблице K = 3, а не 6. Вообщем, проверьте сами.
Здравствуйте. у вас помарка в задании B9.1 NБ = NВ + NД = 6+2 = 8
NГ = NВ + NЕ = 6+3 = 9. В таблице вы эти числа перепутали местами.