B9 математика c ege.yandex.ru

B9.1        B9.2          B9.3          B9.4          B9.5          B9.6          B9.7          B9.8          B9.9          B9.10

B9.11      B9.12        B9.13        B9.14        B9.15        B9.16       B9.17          B9.18         B9.19         B9.20

B9.21      B9.22        B9.23        B9.24        B9.25        B9.26        B9.27        B9.28       B9.29        B9.30  

B9.31      B9.32       B9.33  

Справочные материалы от Д. Гущина 

 

№1

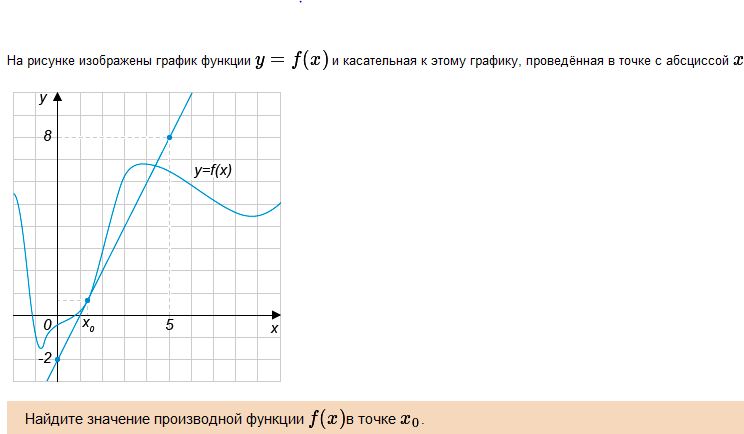Решение. Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки выделены на рисунке жирным и имеют координаты (0, -2) и (5,8) соответственно. Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют длины 5 – 0 = 5 (горизонтальная) и         8 – (-2) = 10 (вертикальная). Тангенс угла наклона касательной t = 10/5 = 2

Ответ  2

№2 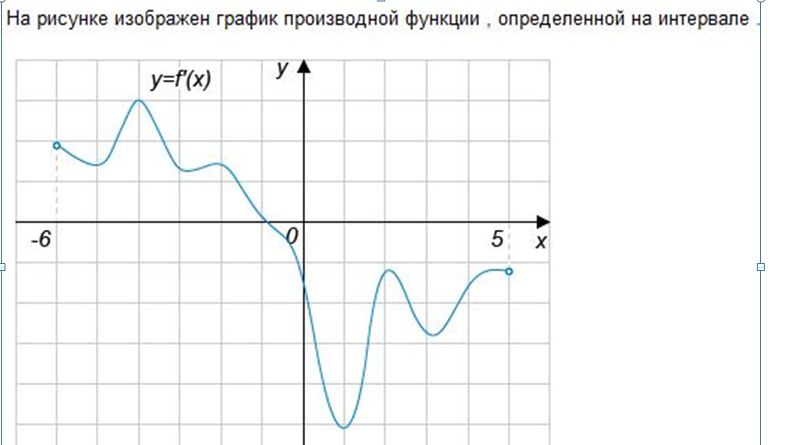  В какой точке отрезка [-5, -1] функция принимает наименьшее значение?

Решение. На рисунке изображен график производной.   Во всех точках отрезка [-5, -1] производная положительна, т.е. функция на отрезке монотонно растет. Значит, наименьшее значение функция принимает на левом краю отрезка – в точке -5.  

Ответ -5

№3   Решение. На рисунке изображен график производной.   Касательная к графику функции f(x) параллельна прямой y = 2x-17 тогда и только тогда, когда производная равна 2. На графике видно, что график пересекает прямую y=2 в двух точках

Ответ 2

№4

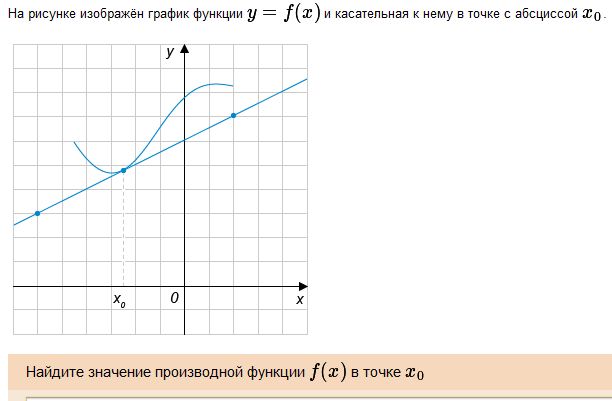Решение Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки выделены на рисунке жирным и имеют координаты (-6, 3) и (2, 7) соответственно. Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют длины 2 – (-6) = 8 (горизонтальная) и         7 – 3 = 4 (вертикальная). Тангенс угла наклона касательной t = 4/8 = 0,5

Ответ 0,5

№5
Решение. В точке касания графиков двух функций выполнены два условия. Во-первых, совпадают значения функций, во-вторых, совпадают значения производных. В данном случае это дает систему двух уравнений с одним неизвестным. Такая система не всегда имеет решение. Это и не удивительно: не всякая прямая имеет с данной кривой точку касания. Посмотрим, что будет в нашей задаче. 1)      Равенство значений функций:

3x+8 = x³+x²-5x -4

2)      Равенство значений производных:

3 = 3*x² + 2x -5

  Решим второе уравнение.

3*x² + 2x -8 = 0

D= 4+96 = 100= 10²

x1 = (-2+10)/6 = 4/3;      x2 = (-2 -10)/6 = -2

Проверим, выполнено ли для этих значений аргумента условие равенства значений функций. Для x=4/3 условие не выполнено; для x =-2 – выполнено (и в том, и в другом убеждаемся подстановкой).

Ответ  -2

 

№6

Решение. Производная отрицательна там, где функция убывает, то есть график функции идет вниз. По условию задачи, нам интересуют пересечения графика с вертикальными линиями сетки. Таких точек на рисунке 4 . А именно: -5, -2, 2, 3.

Ответ  4

 

№7

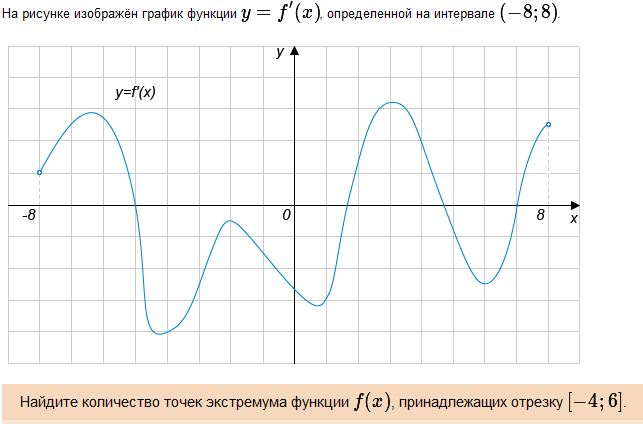Решение. На рисунке изображен график производной.   Экстремумам функции соответствуют точки, в которых производная обращается в 0 и при этом меняет знак. На отрезке [-4, 6] таких точек две.  

Ответ 2

 

№8 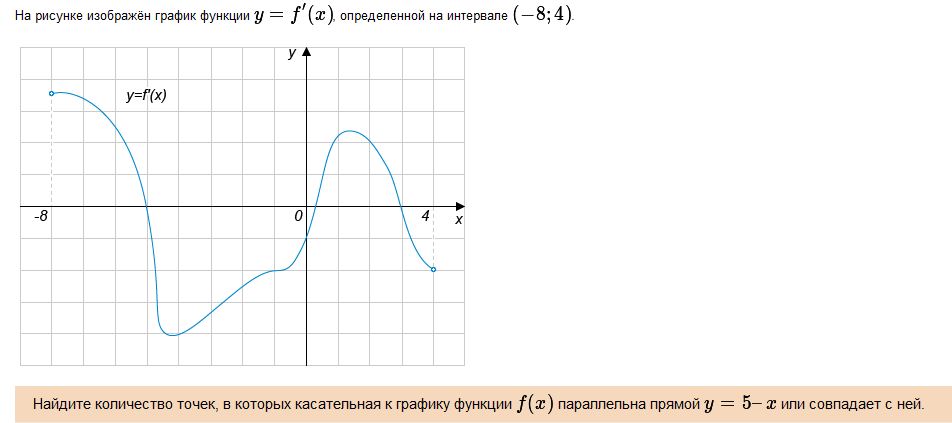Решение. На рисунке изображен график производной.Касательная к графику функции f(x)параллельна прямой  a*x+b в тех точках, где значение производной равно a. В данном случае a = -1. Точек, в которых значение производной равно -1 (т.е. где график производной пересекает горизонталь y=-1) на рисунке 3.

Ответ  3

 

№9 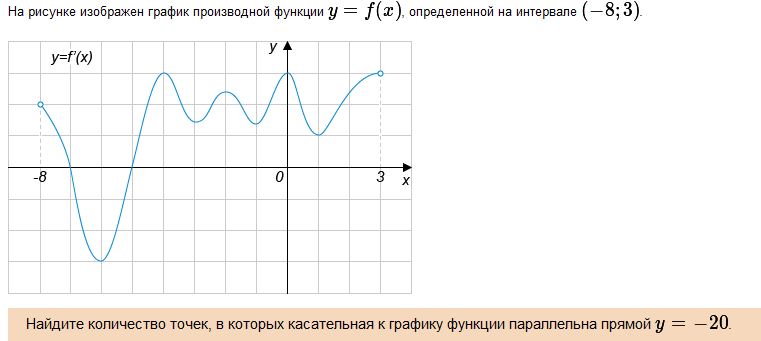Решение. На рисунке изображен график производной.Касательная к графику функции  f(x)   параллельна прямой  a*x+b в тех точках, где значение производной равно a. В данном случае a = 0   [b = -20, но это для решения не важно]. Точек, в которых значение производной равно 0 (т.е. где график производной пересекает ось абсцисс) на рисунке 2.

Ответ 2

 

№10

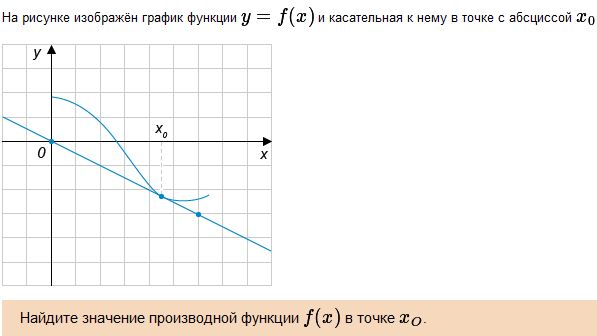Решение. Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки выделены на рисунке жирным и имеют координаты (0, 0) и (6, -3) соответственно (точки перечисляем в порядке возрастания абсцисс). Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют «длины» 6 – 0 = 6 (горизонтальная) и    (-3) – 0 = -3 (вертикальная). Обратите внимание: «длина» вертикальной стороны отрицательна, т.к. большему значению абсциссы соответствует меньшее значение ординаты. Тангенс угла наклона касательной t = (-3)/6 =- 0,5

Ответ -0,5

 

№11

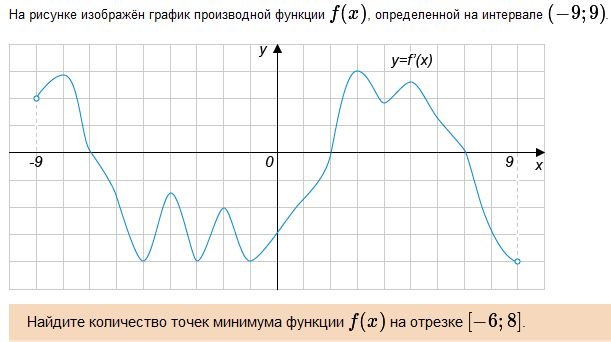Решение. На рисунке изображен график производной.   Минимумам функции соответствуют точки, в которых производная обращается в 0 и при этом меняет знак с минуса на плюс. На отрезке [-6, 8] такая точка одна.

Ответ 1

 

№12

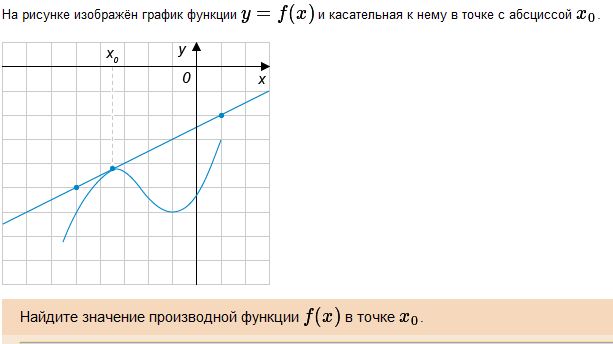Решение.Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки выделены на рисунке жирным и имеют координаты (-5, -5) и (1, -2) соответственно (точки перечисляем в порядке возрастания абсцисс). Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют «длины» 1 – (-5) = 6 (горизонтальная) и    (-2) – (-5) = 3 (вертикальная). Обратите внимание: «длина» вертикальной стороны положительна, т.к. большему значению абсциссы соответствует большее значение ординаты. Тангенс угла наклона касательной t = 3/6 = 0,5

Ответ 0,5

 

№13

Решение. Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки имеют координаты (-4, -4) и (4, -6) соответственно (точки перечисляем в порядке возрастания абсцисс). Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют «длины» 4 – (-4) = 8 (горизонтальная) и    (-6) – (-4) = -2 (вертикальная). Обратите внимание: «длина» вертикальной стороны отрицательна, т.к. большему значению абсциссы соответствует меньшее значение ординаты. Тангенс угла наклона касательной t = (-2)/8 =- 0,25.  

Ответ  - 0,25

.

 

№14

Решение. На рисунке изображен график производной.Касательная к графику функции f(x)параллельна прямой  a*x+b в тех точках, где значение производной равно a. В данном случае a = 1. Точек, в которых значение производной равно 1 (т.е. где график производной пересекает горизонталь y=1) на рисунке 4.

Ответ 4

 

№15

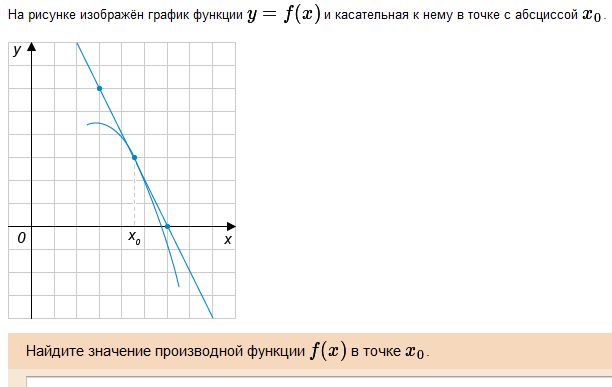Решение. Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки имеют координаты (3, 6) и (6, 0) соответственно (точки перечисляем в порядке возрастания абсцисс). Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют «длины» 6 – 3 = 3 (горизонтальная) и    0 – 6 = -6 (вертикальная). Обратите внимание: «длина» вертикальной стороны отрицательна, т.к. большему значению абсциссы соответствует меньшее значение ординаты. Тангенс угла наклона касательной t = (-6)/3 =- 2.

Ответ -2

 

№16

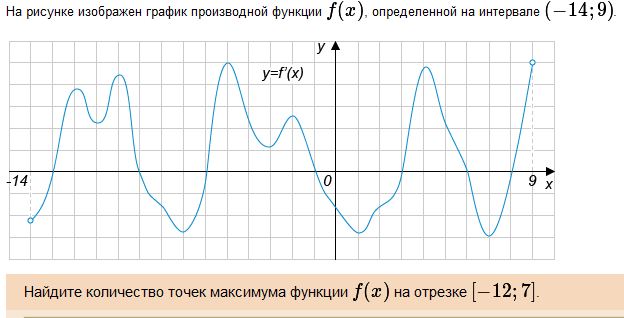Решение. На рисунке изображен график производной.   Максимумам функции соответствуют точки, в которых производная обращается в 0 и при этом меняет знак с плюса на минуса. На отрезке [-12, 7] таких точек три. 

Ответ  3

 

№17

Решение  На рисунке изображен график производной.   Экстремумам исходной функции соответствуют точки, в которых производная обращается в 0.  На отрезке [-9, 7] таких точек четыре.

Ответ  4

Пояснение. Это точки -8, -3, 3 и 5.  В точках -8 и 3 слева от  точки (то есть, при меньших значениях x)  значение производной положительно, а справа от точки (то есть, при больших значениях x)  значение производной отрицательно. Значит, до точки функция растет, а после точки - убывает. Таким образом, точки -8 и 3 - это точки максимума. Аналогично можно понять, что точки -3 и 5 - точки минимума.

 

№18

  Решение Пусть прямая y = 5x-7 касается графика функции y = 6x² + bx -1  в точке x= t. Это означает, что: 1)    Производная к  функции y = 6x² + bx -1  в точке x= tимеет значение 5; 2)    Значения 5t- 7 и 6t² + bt -1 равны. Учитывая, что (6x² + bx -1)’ = 12x-b, получаем систему уравнений c двумя неизвестными b, t: 12t+b= 5                             (1) 6t² + bt -1 = 5t– 7                 (2) Решим эту систему. Из (1) находим: b = 5 – 12t. Подставляем в (2):

6t² + (5 – 12t)*t -1 = 5t – 7

6t² + 5t – 12 t²  -1 = 5t – 7

6t² = 6

t= 1 или t = -1.

По условию,  t < 0, следовательно, t = -1. Из (1) получаем:

12*(-1)  + b = 5

 b = 5 + 12 = 17

 

Ответ  17

 

№19

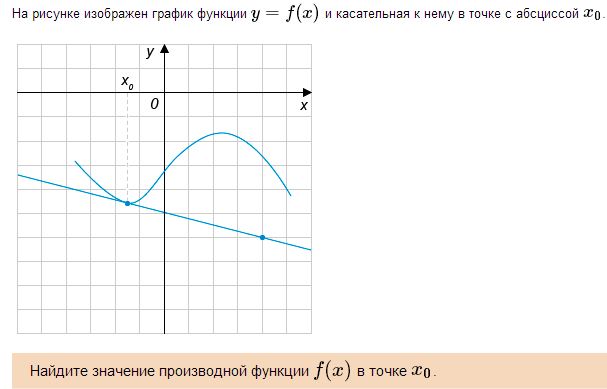 Решение Из рисунка видно, что угловой коэффициент касательной равен -1/4 = -0.25

Ответ -0.25

 

№20 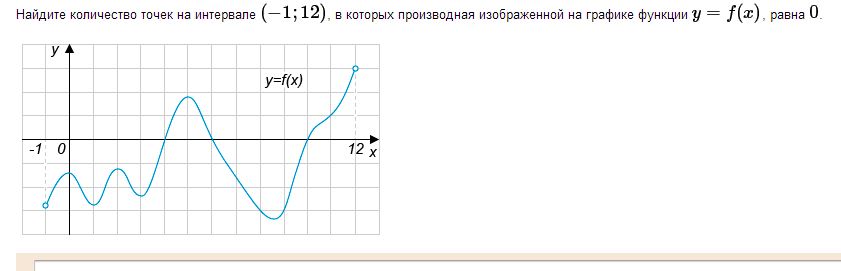Решение Производная обращается в 0 в точках локальных экстремумов, т.е. локальных минимумов и максимумов. На рисунке таких точек шесть: x= 0 (максимум); x= 1 (минимум); x= 2 (максимум); x= 3 (минимум); x= 5 (максимум); x= 9.5 (минимум);

Ответ: 6

Замечание.  Производная элементарной функции обращается в 0 в точках, где касательная параллельна оси Ox. Это не обязательно точки экстремумов. Например, производная функции y = x³ равна 0 при x = 0, но ни минимума, ни максимума в этой точке нет. Но в этой задаче таких  точек нет.

 

 

№21

Найдите касательную к графику функции y=x²+6x−7, параллельную прямой y=5x+11. В ответе укажите абсциссу точки касания.

Решение    Касательная к графику функции y = f(x) в точке x₀ – это прямая с уравнением вида y = f’(x₀)*x+b, где  b– число. [ Это число можно найти, учитывая, что касательная проходит через точку (x₀, f(x₀)), но в этой задаче нам нужно найти только абсциссу точки касания]. В нашем случае f(x) = x²+6x−7. Поэтому

f’(x₀) = 2*x₀ + 6.

Две прямые y = a₁*x + b₁ иy = a₂*x + b₂ параллельны тогда и только тогда, когда a₁ = a₂.  Так как наша касательная параллельна прямойy=5x+11, то для абсциссы точки касания получаем уравнение:

2*x₀ + 6 = 5

            Отсюда  x₀ = (5-6)/2 = -0.5

Ответ -0.5

 

№22 На рисунке изображен график функции y=f(x). Найдите количество целых точек интервала (−2;11), в которых производная функции f(x) положительна.

Решение. Производная f’(x) положительна в тех точках, в которых функция y = f(x) возрастает. Согласно рисунку, на интервале (-2, 11) таких точек 4: точки 1, 2, 3 и 4.

Ответ:4

 

 

№23

Решение. Точка максимума функции y = f(x) – это такая точка, в которой производная f’(x) обращается в 0, причем при переходе через эту точку знак производной меняется с плюса на минус. Согласно рисунку, на отрезке [-11, 0] есть одна такая точка: x = -5.

Ответ:1

Замечание. Точка x = -12 – тоже точка максимума, но она лежит за пределами указанного в задаче отрезка.

 

 

№24 На рисунке изображен график функции y=f(x) , определенной на интервале (−1;13). Определите количество целых точек, в которых производная функции положительна.

Решение. Производная f’(x) положительна в тех точках, в которых функция y = f(x) возрастает. Согласно рисунку, на интервале (-1, 13) таких точек 4: точки  1, 2, 3, 5.

Ответ: 4

 

№25

На рисунке изображен график функции y=f(x), определенной на интервале (−4;10). Определите количество целых точек, в которых производная функции отрицательна.

Решение. Производная f’(x) отрицательна в тех точках, в которых функция y = f(x) убывает. Согласно рисунку, на интервале (-4, 10) таких точек 4: точки 1, 2, 3 и 4.

Ответ:4

 

№26

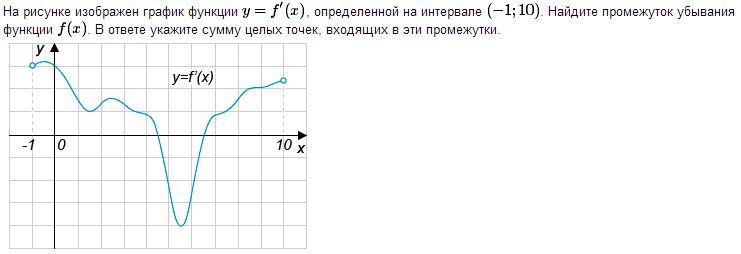
Решение На рисунке - график производной функции f(x). Если не вдаваться в детали, функция убывает в тех точках, в которых производная отрицательна. На рисунке видно, что есть ровно две таких целых точки: x= 5 и x=6. Сумма чисел 5+6 = 11.

Замечание.  Кроме точек, в которых производная отрицательная, дифференцируемая функция f(x) [то есть, функция, у которой во всех точках есть производная] убывает еще и в таких точках, в которых f'(x)=0 и при этом f'(x)<0 слева и справа от точки x. Так обстоит дело, например, с функцией y = x³ при x = 0. На рисунке, к счастью, 🙂 таких точек нет.

Ответ: 11

 

№27

Материальная точка движется прямолинейно по закону , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени t=2с. Ответ дайте в метрах в секунду.

Решение. Нужно найти значение производной  при  [В условии «t=2c» означает, что нужна скорость через 2 секунды от начала отсчета]. Имеем: , 

Ответ: -347

 

№28

Решение. Значение производной с точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент)  касательной в точке x₀.  Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки имеют координаты (1, 1) и (4, -5) соответственно (точки перечисляем в порядке возрастания абсцисс). Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют «длины» 4 – 1 = 3 (горизонтальная) и    (-5) – 1 = -6 (вертикальная). Обратите внимание: «длина» вертикальной стороны отрицательна, т.к. большему значению абсциссы соответствует меньшее значение ординаты. Тангенс угла наклона касательной t = (-6)/3 =- 2.

Ответ -2

 

№29

Решение. Точка, в которой касательная к графику функции y = f(x) параллельна оси абсцисс – это такая точка, в которой производная f’(x) обращается в 0 и при переходе через которую производная f’(x) меняет знак. На рисунке такая точка одна: x = 4.

Ответ:4

Замечание.  На всякий случай напомним. Если знак производной f’(x) при переходе через точку a меняется с плюса на минус, то точка a – точка максимума функции  f(x). Если с минуса на плюс – точка минимума. На рисунке точка 4 – точка максимума.

 

№30

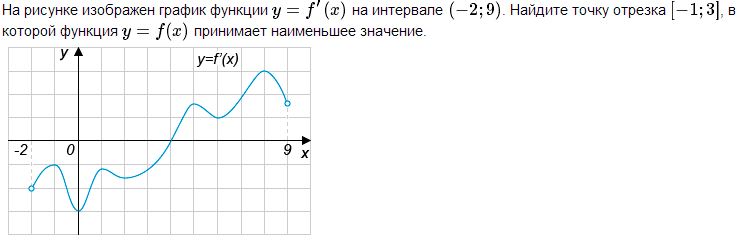Решение. Согласно графику, на всем отрезке [-1, 3] значение производной f’(x) отрицательно. Значит, на всем этом отрезке функция y = f(x) монотонно убывает. Поэтому минимальное значение она принимает на правом конце отрезка, то есть в точке 3.

Ответ: 3

 

№31

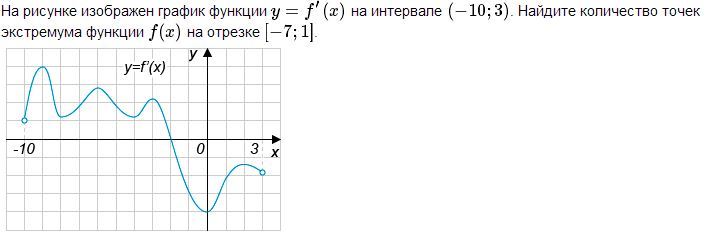Решение. Точка экстремума функции y = f(x) – это такая точка, в которой производная f’(x) обращается в 0. На отрезке [-7, 1] (и вообще на рисунке) такая точка одна: x = -2.

Ответ: 1

 

 

№32

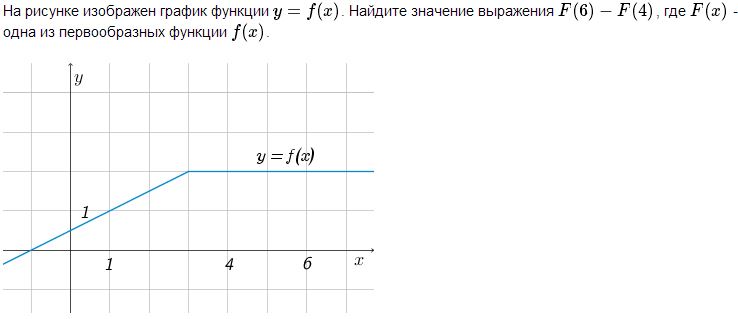Решение. Так как F(x) – первообразная функции y = f(x), то F’(x) = f(x). На участке [4, 6] выполнено: f(x) = F’(x) =2. Поэтому на этом участке F(x) = 2x+c, где c – некоторая константа. То есть, F(6) – F(4) = (2*6+c) – (2*4+c) = 12-8 = 4

Ответ:4

 

№33

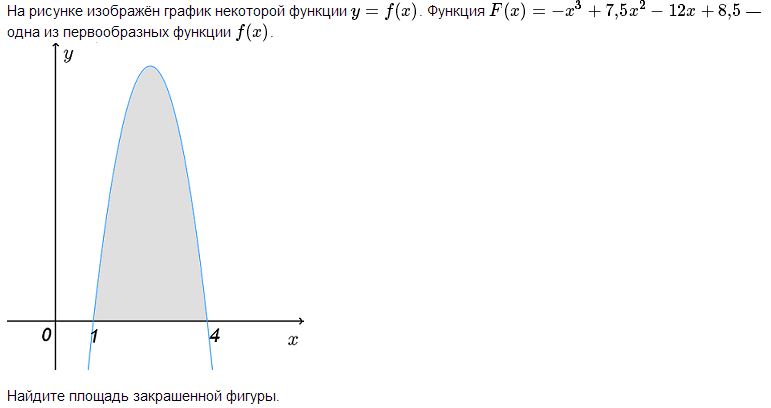Решение. По формуле Ньютона-Лейбница, площадь под графиком функции y = f(x) на отрезке [a,b] равна разности значений первообразной в концах отрезка F(b)-F(a). В нашей задаче имеем: S =  (-4³ +7,5*4² – 12*4 + 8,5)  -  (-1³ +7,5*1² – 12*1 + 8,5)  = = (8 + 8,5)  - (-5,5 + 8, 5) = 8+5,5 = 13,5.

Ответ: 13,5