B5 математика с ege.yandex.ru
B5.1 B5.2 B5.3 B5.4 B5.5 B5.6 B5.7 B5.8 B5.9 B5.10
B5.11 B5.12 B5.13 B5.14 B5.15 B5.16 B5.17 B5.18 B5.19 B5.20
B5.21 B5.22 B5.23 B5.24 B5.25 B5.26 B5.27 B5.28 B5.29 B5.30
Справочные материалы от Д. Гущина
№1
Найдите sinα, если cosα=−\(\) и π<α<\(\)
Решение
\(\)
=> \(\)
из условия: π<α<\(\), или третья четверть, где и синус и косинус отрицательны.
=>\(\)

№2
Найдите значение выражения: \(\)
Решение
\(\)
№3
Найдите значение выражения: \(\).
Решение
\(\)
№4
Найдите значение выражения \(\)
Решение
log11(12,1) + log1110 = log11(12,1*10) = log11(121) = log11(112) = 2
№5
Найдите значение выражения \(\).
Решение
\(\).
№6
Найдите значение выражения
\[\]
.Решение
(4x2−25) / (2x+5) −2x= ((4x2−25) – 2x*(2x+5) ) / (2x+5) = (4x2−25 - 4x2−10x) / (2x+5) = - (10x+25)/ (2x+5) = -5
№7
Найдите 25cos2α, если sinα=−0,7.
Решение
cos(2α) = 1 – 2sin2α = 1 – 2*(-0,7)2 = 1 – 2*0,49 = 1 – 0,98 = 0,02
25* cos(2α) = 25*0,02 = 0,5
№8
Найдите значение выражения
\[\]
.Решение
(6sin27°cos27°) / sin54° = 3*(2sin27°cos27°) / sin54° = 3*sin54° / sin54° = 3
№9
Решение.
Имеем:
\[\]
\[\]
\[\]
№10
Найдите значение выражения \(\), если tga=\(\).
Решение
cos2α = 1/(1+tg2α) = 1/(1+11) = 1/12
36*cos2α = 36*(1/12) = 3
№11
Найдите значение выражения \(\).
Решение
39⋅:65 = 39*26: (35 *25) = 39-5 * 26-5 = 81*2 = 162
№12
Найдите значение выражения \(\).
Решение
\(\).
№13
Найдите значение выражения \(\).
Решение
\(\)
\(\).
№14
Найдите значение выражения: \(\).
Решение
\(\).
№15
Найдите значение выражения \(\).
Решение
\(\)
Ответ 16
№16 Найдите значение выражения: log49 / log649.
Решение. Имеем: log49 = log464 * log649. (см. Примечание после ответа) Поэтомуlog49 / log649 = (log464 * log649) / log649 = log464 = 3
Ответ. 3
Примечание. Докажем формулу logax = logab * logbx
Пусть (ap)q=x. Обозначим apчерез b. Имеем:
x= (ap)q= apq
b = ap
x = bq
Поэтому
logax = pq (1)
logab = p (2)
logbx = q (3)
Из (1), (2) и (3) следует:
logax = logab * logbx
№17
Найдите значение выражения \(\).
Решение
(9+√77) /(√11+√7)2 = (9+√77) /(11+2*√11*√7 + 7) = (9+√77) /(18+2*√77) = ½ = 0,5
Ответ 0,5
№18
Вычислите:
\[\]
.Решение
\(\)
=>\(\)
№19
Найдите значение выражения \(\).
Решение
log7 (4√24) / log7 (24) = log7 (241/4 ) / log7 (24) = ¼ *log7 (24) / log7 (24) = ¼
№20
Вычислите: \(\).
Решение
log7log2128 = log7log2(27) = log77 = 1
Ответ 1
№21
Решение
30*cos33∘/sin57∘ = 30*cos(90∘ - 57∘)/sin57∘ = 30*sin57∘/sin57∘ = 30
Ответ 30
№22
Решение.Обозначим квадратный корень из 13 через r. Имеем:
(7r)*(2r)/(14r-3) = (143) )/(14r-3) = 14r-(r—3)= 143=2744
Ответ 2744
№23
Вычислите log0,52
Решение. Имеем:
0,5 = ½
2 = (½)-1
Поэтому log0,52 = -1
Ответ -1
№24
Вычислите \(\).
Решение
Ответ 25
№25
Вычислите \(\).
Решение Имеем: 216 = 63 = ( (√6)2)3 =(√6)2*3= (√6)6 . Поэтому log√6 (216) = 6 и log2√6 (216) = 62 = 36.
Ответ 36
№26
Решение
Обозначим значение, которое нужно вычислить, через Z.
Имеем: 5+3/5 = 28/5; 12+3/5 = 63/5;
Z = ( √(28/5) - √(63/5) ) / √(7/45) =
= ( √(28/5) / √(7/45) ) – (√(63/5) / √(7/45))
Вычислим отдельно уменьшаемое и вычитаемое.
√(28/5) / √(7/45) = √(28/5 : 7/45) =
= √(28*45/(5*7) = √( (4 *9 )= 2*3 =6
√(63/5) / √(7/45) = √(63/5 : 7/45) =
= √ (63*45/(5*7) = √( 9* 9 )= 9
Таким образом,
Z = 6 – 9 = -3
Ответ -3
№27
Решение
Ответ
№28
Решение . Кубический корень из x обозначается: rt(x).
Имеем:
( rt(6)*rt(4) ) / rt(3) = rt(6*4/3) = rt(4*2) = rt (23) = 2
Ответ 3
№29
Решение
(8+2/11) : (9/11) = (90/11) : (9/11) = (90*11) /(11*9) = 90 / 9 = 10
Ответ
№30
Найдите значение выражения
32z+1:9z:z
при z=1/12.
Решение 9z = (32 ) z = 32z . Поэтому:
32z+1:9z:z = 32z+1:32z:z = 3(2z+1)-2z:z = 32z+1-2z:z = 3:z
При z = 1/12 это равно 3:1/12 = 3*12 = 36
Ответ: 36
№31
Решение.
(√200)* cos2(5π/8) - (√50) = (√50) * ((√4)*cos2(5π/8) – 1) =
= (√50) * (2*cos2(5π/8) – 1) = (√50) * (cos2(5π/8) – sin2(5π/8)) = (√50) * (cos(2*5π/8) = (√50) * (cos(5π/4) = (√50) * (-(√2)/2) = - (√100)/2 = -10/2 = -5
Ответ
№32
Решение.
Ответ 1
№33
Решение.
log2 (4√2) + log312 - log34 = log2 (22+1/2) + log3(12/4) = 2+1/2 + 1 = 3,5
Ответ

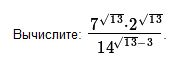
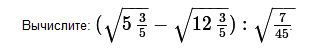
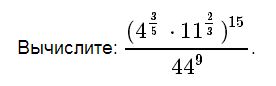

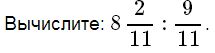
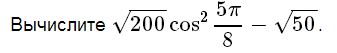

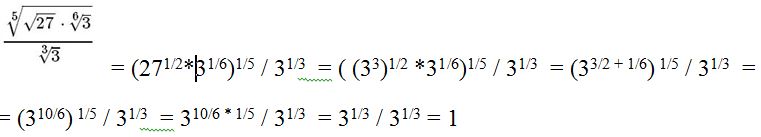

14 комментариев
в 4 задаче же 121 ответ? разве нет?
Нет 🙂 См. решение здесь: http://ege-go.ru/math-ege/b7math/#R1.4
Зачем было в №26 несложное решение записывать в таком громоздком виде.Для школьников такая запись нечитаема,в школе ничего подобного они не видят,а у продвинутых вопроса по поводу такого задания не возникнет
Вы правы. Но, чтобы сделать красиво, нужно возиться с компьютерной версткой. Сейчас лучше?
С другой стороны - разобраться с обозначением sqrt ИМХО вполне посильно и для тех, кто не умеет решать такие задачи
Спасибо за коммент. С Новым Годом!
а почему в девятом номере ответ -0.5?я думала с плюсом должно быть
Возведение в степень буду для (своего 🙂 ) удобства обозначать знаком ^. Например, 2^3 = 8. Логарифм от x по основанию a буду обозначать log(x|a). Например, log(8|2) = 3. Теперь по делу.
Общее правило log(a^k|a^n) = k/n (то есть логарифм от a^k по основанию a^n равен k/n).
Докажу это правило ниже. По этому правилу log (КОРЕНЬ(23)|1/23) = log(23^(1/2)|23^(-1)) = (1/2)/(-1) = -1/2
Проверка. (1/23)^(-1/2) = 1/((1/23)^(1/2))= 1/(1/КОРЕНЬ(23)) = КОРЕНЬ(23)
Теперь про правило. Смотри. Обозначим log(a^k|a^n) через p. Это значит, что (a^n)^p = a^k. Но (a^n)^p = a^(n*p). То есть
a^(n*p) = a^k. Следовательно, n*p = k. То есть, p = k/n.
Разбери сама на примерах. Если что - пиши. Успехов!
Ответ: 0,25. Там 9 находится в знаменателе, его делят на Z, а следовательно Z уходит в числитель, и если её подставить получается деление, а не умножение как у Вас.
Не-не-не! В конце получается 3:z. При z = 1/12 получаем 3:(1/12) = 3*12 = 36. Если непонятно - напиши, я объясню подробнее. Успехов!
мне не понятно №27, №28, №29, "24, "25
Посмотри разборы задач и обсуждение здесь: http://vk.com/topic-45929616_27353856
Теорию можно посмотреть здесь: http://www.berdov.com/docs/logarithm/what/
Если будет непонятно - напиши пож. Успехов!
а по нормальному было сложно оформить минут 20 нужно разбираться если не понял! оформите нормально!!!
Костя, учись нормально общаться. Если в состоянии - напиши понятно, что стоит улучшить. Успехов!
Конечно, 2. 🙂 Спасибо!
Заодно добавили решение для №30
Успехов!
в последнем не три,а два