Задание 15. Пример задания
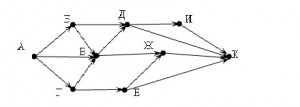
Условие. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение 1. Это решение основывается на следующем правиле.
Правило сложения. Пусть дан ориентрованный граф, не содержащий циклов и из вершины S этого графа выходит 3 ребра: ST1, ST2, ST3. Пусть далее из вершины T1 в вершину Z ведет N1 путей, из вершины T2 в вершину Z ведет N2 путей, из вершины T3 в вершину Z ведет N3 путей. Пусть N – количество путей из вершины S в вершину Z. Тогда
N = N1+ N2+ N3
Это правило, естественно, может быть переформулировано для любого количества ребер, выходящих из данной вершины.
Для того, чтобы найти количество путей, ведущих из вершины А в вершину К, мы найдем количество путей, ведущих в К, для каждой вершины. Вершины будем перебирать, двигаясь «от конца к началу» - от К к А. Говоря более точно, если есть путь, ведущий из вершины X в вершину Y, то вершина Y должна быть просмотрена раньше вершины X. Например, можно перебирать вершины в таком порядке:
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей |
Обратите внимание: вершину В нужно просмотреть раньше, чем вершины Б и Г, поскольку в графе есть ребра БВ и ГВ. А в каком порядке рассматривать вершины в парах И и Ж или Е и Д – не важно.
Из вершины К есть ровно 1 путь в саму эту вершину («пустой» путь, путь из 0 ребер). Далее можно всюду пользоваться описанным правилом. Но в нашем случае для вершин И, Ж, Е и Д количество путей можно увидеть из рисунка (см. следующую таблицу):
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 2 | 2 |
А дальше, чтобы не запутаться, лучше использовать правило. Получим:
NВ = NД + NЖ = 2+1 = 3
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 2 | 2 | 3 |
NБ = NВ + NД = 3+2 = 5
NГ = NВ + NЕ = 3+2 = 5
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 5 |
NА = NБ + NВ + NГ = 5+3+5 = 13
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| К-во путей | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 5 | 13 |
Ответ: 13
Решение 1а (более короткая запись). Добавим в таблицу еще одну строку («Куда идем»). В этой строке укажем, в какие вершины ведут ребра из данной вершины.
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| Куда идем | - | К | К | Ж,К | И,К | Д,Ж | В,Е | В,Д | Б,В,Г |
| К-во путей | 1 |
В строке «К-во путей» можно сразу заполнить количество путей для вершины К (1 путь, в котором 0 ребер). Дальше заполняем таблицу слева направо, пользуясь правилом сложения и глядя в строку «Куда идем».
| № просмотра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вершина | К | И | Ж | Е | Д | В | Г | Б | А |
| Куда идем | - | К | К | Ж,К | И,К | Д,Ж | В,Е | В,Д | Б,В,Г |
| К-во путей | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 5 | 13 |
Например, 7-й столбец (вершина Г) заполняем так. В строке «Куда идем» - 2 вершины В, Е. Значит, по правилу сложения,
NГ = NВ + NЕ = 3 +2=5
Количества путей NВ, NЕ для вершин В, Е были записаны в строку «К-во путей» раньше.
Ответ: 13 Замечание. Самое трудное при таком решении – правильно определить порядок просмотра вершин и не ошибиться, заполняя строку «Куда идем». Вычисления при заполнении строки «К-во путей» несложные.Решение 2. Это решение состоит в том, чтобы просто выписать все пути из А в К в алфавитном порядке. Начнем с того, что выпишем все ребра, выходящие из А:
Шаг 1.
АБ
АВ
АГ
Любой путь из А в К является продолжением одного из путей нашего списка. Очередной шаг нашего алгоритма будет состоять в том, чтобы продолжить первый по алфавиту незаконченный путь из нашего списка.
Замечание. Можно считать, что мы начали с «пустого пути» из А в А и уже применили эту процедуру на прошлом шаге. Добавленные на очередном шаге пути будем подчеркивать. Итак.
Шаг 2. Продолжаем путь АБ.
АБВ
АБД
АВ
АГ
Шаг 3. Продолжаем путь АБВ.
АБВД
АБВЖ
АБД
АВ
АГ
Замечание. У нас появилось два пути, ведущие в точку Д. Понятно, что у них одинаковое количество продолжений. Этим можно воспользоваться (мы это и делали в решении 1, когда сначала вычисляли количество путей из в Д в К, а только потом – количества путей из В и Д).В этом решении мы этого не делаем – ради простоты рассуждений.
Шаг 4. Продолжаем путь АБВД. Появился полный путь - путь из А в К. Такие пути будем выделять жирным шрифтом.
АБВДИ
АБВДК
АБВЖ
АБД
АВ
АГ
Шаг 4. Продолжаем путь АБВДИ – этот путь закончен.
АБВДИК
АБВДК
АБВЖ
АБД
АВ
АГ
Шаг 5 . Продолжаем и заканчиваем путь АБВЖ. Можно заметить, что мы выписали все пути из В в К: ВДИК, ВДК, ВЖК.
АБВДИК
АБВДК
АБВЖК
АБД
АВ
АГ
Шаги 6, 7 . Продолжаем путь АБД – получим два полных пути АБДИК и АБДК. Мы уже знаем, что из Д в К ведут два пути: ДИК и ДК.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВ
АГ
Замечание. Мы выписали все пути, которые проходят через Б. В соответствии с решением 1, их оказалось 5.
Шаг 8 . Продолжаем путь АВ.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВД
АВЖ
АГ
Шаги 9, 10 . Продолжаем путь АВД - получаем еще два полных пути.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВДИК
АВДК
АВЖ
АГ
Шаг 11 . Продолжаем путь АВЖ - получаем еще один полный путь. Всего три пути через В.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВДИК
АВДК
АВЖК
АГ
Замечание. Можно было вспомнить, что из В в К есть три пути ВДИК, ВДК, ВЖК. И сделать шаги 8 - 11 за один шаг.
Шаг 12. Продолжаем путь АГ.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВДИК
АВДК
АВЖК
АГВ
АГЕ
Шаг 13. Продолжаем путь АГВ. Можно делать это как и раньше – по одному ребру. А можно заметить, что из В в К есть ровно три пути: ВДИК, ВДК, ВЖК. И сразу добавить эти три продолжения.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВДИК
АВДК
АВЖК
АГВДИК
АГВДК
АГВЖК
АГЕ
Шаги 14, 15. Продолжаем путь АГЕ. Из Е есть два пути в К: ЕЖК и ЕК. Соератим время и напишем их сразу.
АБВДИК
АБВДК
АБВЖК
АБДИК
АБДК
АВДИК
АВДК
АВЖК
АГВДИК
АГВДК
АГВЖК
АГЕЖК
АГЕК
Все пути выписаны.
Ответ: 13
Замечание. Время работы второго алгоритма пропорционально общему количеству путей из А в К. Для больших графов оно не годится. Но если путей немного (как в нашем случае), им можно воспользоваться - из-за наглядности.


13 комментариев
Предлагаю ещё решение, по мне оно проще.
- Считаем варианты путей из вершин, следующих за А (БВГ) и не заходящие в друг в друга.Б2/В3/Г2
- Считаем варианты, приводящие к этим вершинам Б1/В3/Г1
- Считаем ответ 2*1+3*3+2*1=13
Записывать варианты в ответе не требуется и тормозит решение. Можно брать произвольные промежуточные вершины, те, которые удобны, нравятся, приглянулись и пр.
Очень хорошее наблюдение! По идее правильно, но есть нюансы. Давай я напишу все это чуть более аккуратно.
1. Назовем группу вершин сечением, если любой путь из A в Z проходит через одну из вершин этой группы. В качестве аналога группы (БВГ) можно брать только сечения, а не «брать произвольные промежуточные вершины, те, которые удобны, нравятся, приглянулись и пр». Используя сечения, мы не потеряем ни одного пути. Например, группу (ЕЖИ) брать нельзя.
2. Другая проблема в том, чтобы не посчитать один путь два раза. Например, мы могли бы (если бы плохо считали) путь АБВЖК два раза – и как путь через Б, и как путь через В. Эту проблему ты решил правильно – для каждой вершины сечения рассматриваем только такие пути, на которых ПОСЛЕ этой вершины нет других вершин сечения.
3. А теперь – главное: как считать количество «правильных» путей через каждую из вершин сечения? В нашем случае это видно на глаз. Поэтому, как ты правильно пишешь, все получается просто. А если граф будет побольше? Тогда придется использовать один из описанных на сайте способов. Или строить новые сечения . Но в этом случае, чтобы решение было алгоритмическим (т.е. его можно было бы формально применить к любому графу), нужно написать, как именно следует выбирать сечения. Если хочешь, попробуй это сделать. Я думаю, получится что-то похожее на решение 1 (с заполнением таблицы).
4. И последнее. Два приведенных способа (с построением таблицы и построением всех путей) – алгоритмические. Оба они правильно решают задачу, но затрачивают совершенно разное время. При построении таблицы время работы алгоритма пропорционально количеству ребер в графе, а при построении всех путей – пропорционально колмчеству путей.
Такие дела. Пиши еще – что написать подробнее, какие есть соображения
Успехов!
по п.3 К этому примеру обратился после аналога в КИМ Демо 2014. Там вершин больше, но в ответе у учителя почему-то путей меньше. (Есть ли они официально, эти ответы? Не нашёл.) Значит разрабы усложнили простую задачу. Это меня так сильно огорчило, что пришлось заняться конкретно. Ессно, брать вершины из которых по одному/два пути неинтересно, но вполне корректно. Умножение на единицу - да пожалуйста. Вы пробовали сравнивать время решения по этому способу с указанным в спецификации. Железно он не проходит, так что, каким бы правильным формально не был, советовать его бесполезно. Во всяком случае, своему ребёнку его не советую, обязательно ошибётся в суете и возбуждении. Легче пропустить. Для ЕГЭ точных наук важен автоматизм.
Отвечаю по пунктам.
1. Ответ в B9 из демо 2014: 23. Чтобы убедиться в этом, можно выписать все пути в алфавитном порядке (как в решении 2). Но решать лучше 1-м способом.
2. То, что написано дальше - не понял 🙁 О каком "способе, указанном в спецификации" идет речь? В какой спецификации? Уточните, пож.
3. Ребенку я бы советовал использовать 1-й из двух описанных на сайте способов. Если не бояться ошибиться, можно количества путей из вершины в "выход" (по-научному - "сток") писать прямо на картинке. Получается быстро. Удачи!
Попробуйте сравнить время решения и вопрос отпадёт. Только на запись уходит кучу времени, а вдруг почерк подведёт? ведь всё решается в нервозной обстановке. Есть такой документ к КИМ ЕГЭ, спецификация называется. Точно не помню, но там есть примерное (нормативное) время решения для задач. Возможно, мне это навеяло. А что касаемо советов. На то он и сайт, можно выбрать то, что больше приглянулось
В конечном счете, Вам решать, что советовать Вашему ребенку. Могу только повторить: Ваше наблюдение про использование "сечений" совершенно правильное и помогает, если граф небольшой. Рецепта, который можно применить к графу произвольного размера, оно не дает. На мой вопрос, как "алгоритмизировать" Ваше решение, Вы не ответили. Я думаю, что, если сделать это аккуратно, то получится что-то вроде 1-го метода решения (хотя возможны варианты).
Настоятельно советую Вашему ребенку разобраться в 1-м способе решения ("по-научному" это метод динамического программирования).
Успехов!
PS "А что касаемо советов. На то он и сайт, можно выбрать то, что больше приглянулось"
=== Никаких проблем 🙂 Используйте то, что нравится. Ваши вопросы и замечания помогают нам делать сайт лучше и ИМХО помогают другим посетителям. Пишите еще!
PPS Про спецификацию понял. Там есть только общее время на экзамен, время решения отдельных задач не регламентируется. См. у нас на сайте спецификацию ЕГЭ и спецификацию ГИА. По прикидкам, на B13 можно потратить минут 5-7. Этого хватает при использовании 1-го метода.
Сильно извиняюсь, но из Д в Ж пути нет (1я строка ответа) или это плохое разрешение картинки. Появился на шаге 9/10 без объяснений сам собой. Как минимум одного пути недостаёт
Спасибо! Опечатки исправили. Успехов!
Не до конца, в ш. 12 осталось
в решении 2 в 3ем шаге строчка
p align=»center»
а так все задания расписаны идеально! если б знал раньше об этом сайте то всё было бы отлично!!! а так придётся всю ночь учить)))
Спасибо! Баг исправил. Если есть вопросы - пиши. А то я иду спать 🙂
И тебе стоит перед экзаменом отдохнуть и быть на экзамене бодрым 🙂 Удачи!
да спасибо)
а вы сайт сами делали или вам помогали??
Конечно, не сам! На сайте написано (где "О проекте"): дизайн и веб-мастеринг Катерина Чухонцева. Я, как ученый медведь, - умею то, чему меня научила Катерина.:)
Помогает Александр Чемерис. Например, вчера, когда сайт начал тормозить, Саша разобрался и для подстраховки создал возможность работы с другого сервера. К счастью, не пригодилось. Еще Саша по совету Андрея Михеева прикрутил Яндекс.Метрику - очень полезно для отслеживания работы сайта. Сашины советы по жизни в Интернете всегда очень помогают.
Много народу помогает по контенту. Разбор нескольких заданий сделал С.С. Крылов, я его потом только "причесал". Еще помогали Я.Н.Зайдельман (Переславль), В.Р.Лещинер, С.Ф.Сопрунов (Москва), Ася Ройтберг (Пущино), Д.М.Ушаков (С.-Петербург), К.Ю.Поляков (мы изучили его материалы, когда создавали сайт), другие люди (кого забыл - извините 🙂 ). И все, кто сообщал об ошибках и давал советы в комментах. СПАСИБО!
Вообще сайт задуман, как открытая разработка (примерно, как Википедия, но, наверное, с большим модерированием) - и для учеников, и для взрослых.
Посмотрим, что из этого вырастет 🙂 Удачи на экзамене и вообще!