B15 Математика
B15.1 B15.2 B15.3 B15.4 B15.5 B15.6 B15.7 B15.8 B15.9 B15.10
B15.11 B15.12 B15.13 B15.14 B15.15 B15.16 B15.17 B15.18 B15.19 B15.20
B15.21 B15.22 B15.23 B15.24 B15.25 B15.26 B15.27 B15.28 B15.29 B15.30
B15.31
Справочные материалы от Д. Гущина
№1
Центральный угол на 36∘ больше острого вписанного угла, опирающегося на ту же дугу окружности.

Решение
Пусть вписанный ∠ AСB=x, тогда центральный ∠AOB=2x (т.к. вписанный угол равен половине центрального угла, опирающиеся а одну дугу)
|∠ACB-∠AOB|=|x-2x|=x=36
Ответ 36
№2
Диагонали ромба равны 16 и 30. Найдите длину стороны ромба.

Решение
Найдем сторону по теореме Пифагора.
первая диагональ -\(\) вторая-\(\)
\(\)
=>a=17
Ответ 17
№3
В треугольнике ABC угол C равен 90°, cosB=\(\). AB=29. Найдите AC.
Решение
\(\)
\(\)
sinB=\(\)
AC=AB*sinB=21
Ответ 21
№4
Решение
tgA=\(\)=>CB=3x AB=4x
По теореме Пифагора
AC=\(\)=5x
=>sinA=\(\)
Ответ 0,6
№5
Решение
см №3
Ответ 1,4
№6
В прямоугольном треугольнике АВС катеты равны 15 и 6. Найдите тангенс острого угла при большем катете.
Решение
Тангенс при меньшем угле-меньше.
\(\)
Ответ 0,4
№7
Найдите косинус острого угла равнобедренной трапеции, основания которой равны 37 и 49, а боковые стороны — 15.
Решение
построим высоту равнобедренной трапеции BH. Получим прямоугольный треугольник ABH.
Гипотенуза треугольника- боковая сторона трапеции (AB)
малый катет равен полуразности оснований трапеции AH=(AD-BC):2=(49-37):2=6
=> \(\)
Ответ 0,4
№8
Решение
треугольник угол А, угол B и угол C
угол A=46
угол B=180-127 (тк внешний =127)
угол C=180-A-B=180-46-180+127=127-46=81
Ответ: 81
№9
В треугольнике ABC угол C равен 90∘, sinA=\(\), AC=\(\). Найдите AB.
Решение
см №3
Ответ 28
№10
В треугольнике ABC угол A равен 90∘, tgB=\(\), AC=5. Найдите BC.
Решение
см №4
Ответ 10
№11
В треугольнике ABC угол C равен 90∘, tgA=\(\), BC=4. Найдите AB.
Решение
см №4
Ответ 12
№12
В треугольнике ABC угол C равен 90∘, AC=3, sinA=\(\). Найдите BC.
Решение
см №3
Ответ 2,25
№13
В треугольнике ABC угол C равен 90∘, AB=40, AC=\(\). Найдите sinA.
Решение
\(\)
\(\) тк a+b=\(\)
=> \(\)
Ответ 0,7
№14
В треугольнике ABC угол C равен 90∘, cosA=\(\). Найдите tgA
Решение
см №4
Ответ 2
№15
Два угла треугольника равны 74∘ и 41∘. Найдите угол (острый), который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Решение
Ответ 65
№16
В треугольнике ABC угол C равен 90∘, AB=14,AC=\(\). Найдите sinA.
Решение
см №4
Ответ 0,5
№17
В треугольнике ABC AB=BC, AC=24, cos∠C=\(\). Найти высоту BH.
Решение
Треугольник ABC-равнобедренный, следовательно высота BH проведенная к основанию треугольника является также медианой.
=>CH=AH=AC:2=12
\(\) => треугольник HBC-египетский =>BH=\(\)12=4*4=16
Ответ 16
№18
Прямые, содержащие высоту CH и биссектрису AD треугольника ABC, пересекаются в точке O, ∠BAD=63∘. Найдите угол OAC. Ответ дайте в градусах.
Решение

Отметим, что угол BAC = 2*(угол BAD) = 2*\(\) = \(\) - то есть это тупой угол. Поэтому чертеж выглядит так, как изображено на рисунке.
угол OAC=угол HAO+угол HAC
угол BAD=углу HAO=\(\) (вертикальные)
угол HAC=\(\)-угол СAB=\(\)
OAC=63+54=\(\)
Ответ 117
№19
Основания равнобедренной трапеции равны 78 и 60. Тангенс острого угла равен \(\). Найдите высоту трапеции.
Решение
Ответ 2
№20
В равнобедренном треугольнике ABC угол при вершине C равен 30∘, а боковые стороны AC=BC=72. Найдите высоту AH.

Решение
№21
Хорда AB делит окружность на две части, градусные величины которых относятся как 13 к 59. Под каким углом видна эта хорда из точки C, если она принадлежит меньшей дуге окружности? Ответ дайте в градусах.

Решение
№22
Вокруг четырехугольника ABCD можно описать окружность. Найдите угол CAD, если ∠ABC=50∘и ∠ABD=33∘. Ответ дайте в градусах.

Решение
В параллелограмме ABCD cos∠BAD=\(\) . Найдите sin∠ADC.

Решение ∠ ADC = 180° - ∠ BAD. Следовательно, sin ∠ ADC = sin∠ BAD = √(1- cos² ∠ BAD) = √(1-624/625) = √(1/625) = 1/25.
Найдите медиану треугольника ABC, проведенную из вершины B, если AB=AC=\(\), BC=\(\).

Решение
В треугольнике ABC отрезок AD - биссектриса угла A, угол C равен 24∘, угол CAD равен 29∘. Найдите угол B. Ответ дайте в градусах.

Решение
№26
В прямоугольном треугольнике ABC с прямым углом C, гипотенуза AB равна \(\), а sinA=0,2. Найдите длину высоты CH.
Решение
Биссектрисы углов B и C параллелограмма ABCD пересекаются на стороне AD в точке E. Сторона AB равна 2. Найдите BC.

Решение
В прямоугольном треугольнике ABC с прямым углом C, тангенс внешнего угла при вершине A равен \(\) , сторона BC равна 3. Найдите сторону AB.
Решение
Ответ 7
№29
Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 36∘? Ответ дайте в градусах.

Решение
Сумма противолежащих углов равнобедренной трапеции равна \(\)
Пусть ∠A=x∘=> ∠C=\(\)
∠A+∠C=2x+36=180
2x=180-36=144
x=72=> больший угол C=x+36=72+36=108
Ответ 108
№30
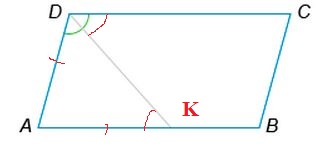
Биссектриса тупого угла D параллелограмма ABCD делит сторону AB в отношении 5 к 8, считая от вершины A. Найдите большую сторону параллелограмма, если его периметр равен 18.

Решение
Пусть K– точка пересечения биссектрисы DKи отрезка AB (см. рисунок).
1. Углы KDCи DKA равны (накрест лежащие углы при DC || AB и секущей DK. Углы KDCи KDAравны, так как KD– биссектриса. Значит углы DKA и KDA тоже равны.
2. В треугольнике DKAуглы при основании DKравны (см. п.1). Значит, этот треугольник равнобедренный и DA = AK.
3. Обозначим длину стороны DA (меньшей из сторон) через x; длину стороны ABчерез y. По доказанному (см. п.2) AK = AG = x. Следовательно, KB = y-xи по условию задачи получаем:
x: (y-x) = 5 : 8 (1)
Так как, периметр параллелограмма равен 18, получаем:
2*(x+y) = 18 (2)
4. Решаем систему (1) - (2). Из (1) :
8*x = 5*(y-x)
8x = 5y– 5x
5y = 13x
y= (13/5)*x (3)
Подставляем из (3) в (2)
2 * (x+ (13/5)*x) = 18
(18/5)*x = 9
x= 2,5
Из (3) находим: y = (13/5)*2,5 = 13/2 = 6,5
Ответ 6,5
№31
Сторона AB тупоугольного треугольника ABC в \(\) раз больше радиуса описанной около него окружности. Найдите угол C . Ответ дайте в градусах.

Решение
Ответ


7 комментариев
№18
Прямые, содержащие высоту CH и биссектрису AD треугольника ABC, пересекаются в точке O, ∠BAD=63∘. Найдите угол OAC. Ответ дайте в градусах.
Углы смежные, чего там высчитывать? 180-63=117
когда решение 30 будет?
Выложили. См. http://ege-go.ru/math-ege/b6math-2/#R1.30
Удачи!
Когда будут варианты ПОЛНОСТЬЮ прорешены? Некоторые задания я сам не могу разобрать. Типа В8 в 23 варианте.
Решение №23 выложили. Если что-то непонятно - напиши.
Остальные - по мере возможности (сейчас каникулы 🙂 )
Пиши, в чем есть потребность - будем выкладывать. Успехов!
Спасибо - мы добавили пояснение в РЕШЕНИЕ.
Вы правы - если бы угол BAC был острый, и чертеж, и ответ были бы другими. Однако в условие ничего добавлять не нужно. То, что угол BAC тупой следует из того, что его половина равна 63 градуса.
С Новым Годом!
В условии задачи №18 надо указать, что угол ВАС тупой, иначе могут быть два чертежа и два совершенно разных ответа.