Эквивалентные преобразования логических выражений

При решении различных логических задач полезно выполнять эквивалентные преобразования логических выражений – так же, как при решении алгебраических задач полезно выполнять эквивалентные преобразования алгебраических выражений.

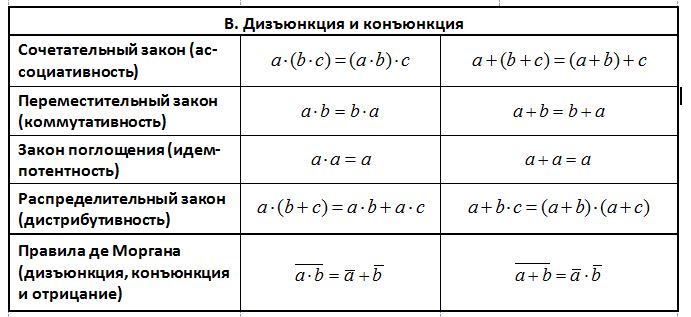
В то же время есть и существенные различия между преобразованиями логических и алгебраических выражений. В алгебре есть устоявшийся список тождественных преобразований выражений – так называемые формулы сокращенного умножения (квадраты и кубы суммы и разности; разность квадратов, сумма и разность кубов), а также формулы, связанные с определением степени и основными законами сложения и умножения (сочетательный, переместительный, распределительный). В курсе логики аналогом такого списка можно считать набор формул, приведенный в таблице 1. Но это только наше мнение – правда, основанное на опыте преподавания информатики 🙂   Деление формул в таблице на группы – условное и приведено лишь для удобства восприятия. Желательно уметь пользоваться этими формулами так же свободно, как и алгебраическими формулами сокращенного умножения. В ЕГЭ по информатике умение преобразовывать логические выражения проверяется в задаче 18.

Примечание. В таблицах использована «алгебро-подобная» система обозначений логических операций. Конъюнкция (логическое умножение) и дизъюнкция (логическое сложение) обозначаются символами «·» и «+» соответственно, а отрицание – чертой сверху. Эти обозначения общеприняты  среди инженеров (но не специалистов по математической логике :)) и используются в некоторых школьных учебниках, в частности, в учебниках К.Ю.Полякова и Е.А.Еремина

Таблица 1.