Выбор отрезка, для которого истинно универсальное высказывание. Базовые задачи с решениями
К каждой задаче полезно нарисовать рисунок – числовую ось с отмеченными отрезками. Нарисуйте эти рисунки самостоятельно.
Если не получится – пишите.
A10.1
Варианты ответов:
1) [8, 20]
2) [12. 24]
3) [16, 28]
4) [18, 32]
Правильный вариант: 4
Решение:
Формула верна при любом значении переменной x тогда и только тогда, когда отрезок P целиком лежит внутри отрезка A. Этому условию удовлетворяет только отрезок [18, 32].
Ответ: [18, 32] (вариант 4).
A10-2
Варианты ответов:
1) [11, 31]
2) [21, 41]
3) [31, 51]
4) [41, 61]
Правильный вариант: 2
Решение:
Формула верна при любом значении переменной x тогда и только тогда, когда отрезок A целиком лежит внутри отрезка P. Этому условию удовлетворяет только отрезок [21, 41].
Ответ: [21, 41] (вариант 2).
A10-3
Варианты ответов:
1) [51, 72]
2) [62, 83]
3) [73, 94]
4) [84, 105]
Правильный вариант: 2
Решение 1:
Формула эквивалентна формуле (x Î A) → (x Î P). Эта формула верна при любом значении переменной x тогда и только тогда, когда отрезок A целиком лежит внутри отрезка P. Этому условию удовлетворяет только отрезок [62, 83].
Решение 2:
Формула верна при любом значении переменной x тогда и только тогда, когда ¬(x Î A) истинно везде, где (x Î P) ложно (и, возможно при некоторых значениях x, для которых (x Î P) истинно). Последнее означает, что отрезок A целиком лежит внутри отрезка P. Этому условию удовлетворяет только отрезок [62, 83].
Ответ: [62, 83] (вариант 2).
A10-4
Варианты ответов:
1) [31, 52]
2) [43, 64]
3) [55, 76]
4) [67, 98]
Правильный вариант: 3
Решение 1:
Формула эквивалентна формуле (x Î P) → (x Î A). Эта формула верна при любом значении переменной x тогда и только тогда, когда отрезок P целиком лежит внутри отрезка A. Этому условию удовлетворяет только отрезок [55, 76].
Решение 2:
Формула верна при любом значении переменной x тогда и только тогда, когда (x Î A) истинно везде, где ¬(x Î P) ложно, т.е. (x Î P) истинно (и, возможно при некоторых значениях x, для которых (x Î P) ложно). Последнее означает, что отрезок A целиком содержит отрезок P. Этому условию удовлетворяет только отрезок [55, 76].
Ответ: [55, 76] (вариант 3).
A10-5
Варианты ответов:
1) [51, 72]
2) [62, 83]
3) [73, 94]
4) [84, 105]
Правильный вариант: 3
Решение 1:
Формула тождественно ложна тогда и только тогда, когда ее отрицание тождественно истинно. Используя правило де Моргана, получим, что отрицание исходной формулы эквивалентно формуле
(x Î P) \/ ¬ (x Î A)
Последняя формула, в свою очередь, эквивалентна формуле
(x Î A) → (x Î P).
Эта формула верна при любом значении переменной x тогда и только тогда, когда отрезок A целиком лежит внутри отрезка P. Этому условию удовлетворяет только отрезок [73, 94].
Решение 2:
Формула ложна при любом значении переменной x тогда и только тогда, когда (x Î A) ложно везде, где ¬(x Î P) истинно, т.е. (x Î P) ложно (и, возможно при некоторых значениях x, для которых (x Î P) истинно). Последнее означает, что отрезок A целиком лежит внутри отрезка P. Этому условию удовлетворяет только отрезок [73, 94].
Ответ: [73, 94] (вариант 3).
A10-6
Варианты ответов:
1) [51, 72]
2) [62, 83]
3) [73, 94]
4) [84, 105]
Правильный вариант: 3
Решение 1:
Формула тождественно ложна тогда и только тогда, когда ее отрицание тождественно истинно. Используя правило де Моргана, получим, что отрицание исходной формулы эквивалентно формуле
¬ (x Î P) \/ (x Î A)
Последняя формула, в свою очередь, эквивалентна формуле
(x Î P) → (x Î A).
Эта формула верна при любом значении переменной x тогда и только тогда, когда отрезок P целиком лежит внутри отрезка A. Этому условию удовлетворяет только отрезок [73, 94].
Решение 2:
Формула ложна при любом значении переменной x тогда и только тогда, когда ¬(x Î A) ложно везде, где (x Î P) истинно (и, возможно при некоторых значениях x, для которых (x Î P) ложно). То есть (x Î A) истинно везде, где (x Î P) истинно Последнее означает, что отрезок P целиком лежит внутри отрезка A. Этому условию удовлетворяет только отрезок [73, 94].
Ответ: [73, 94] (вариант 3).

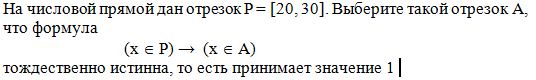
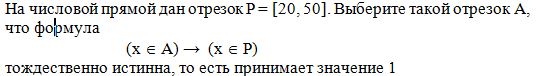
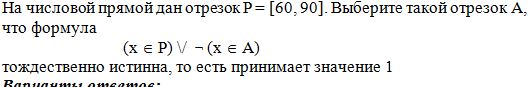
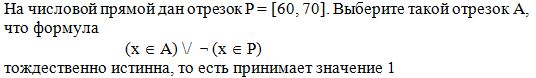
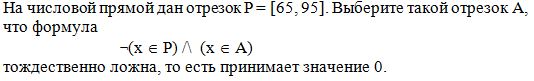
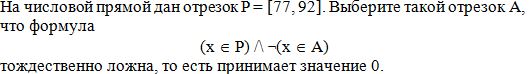

1 Коммент
[...] с демо-2013. Там пока не все, что планировалось. Но есть базовые задачи, к которым, как правило, сводятся подобные задачи. [...]